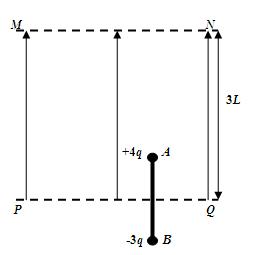
如图所示，在真空中的竖直平面内，用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B，A球的电荷量为+4q，B球的电荷量为—3q，组成一带电系统。虚线MN与PQ平行且相距3L，开始时PQ恰为杆的中垂线。在MN与PQ间加竖直向上的匀强电场，恰能使带电系统静止不动。现使电场强度突然加倍（已知当地重力加速度为g），求：
（1）B球刚进入电场时的速度v₁的大小；
（2）B球的最大位移及从开始静止到最大位移处B球电势能的变化量；
（3）带电系统运动的周期T。