质量为m的小物块,用轻弹簧固定在斜面体上,斜面的倾角为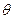 ,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
(1)若斜面光滑,电梯静止时弹簧的伸长量为x.如果电梯竖直向上做匀加速直线运动,弹簧的伸长量为2 x.求电梯竖直向上加速运动时的加速度.
(2)若斜面不光滑,斜面与物块之间的动摩擦因数为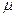 ,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)
,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)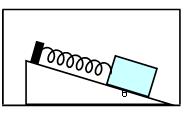
质量为m的小物块,用轻弹簧固定在斜面体上,斜面的倾角为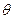 ,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
(1)若斜面光滑,电梯静止时弹簧的伸长量为x.如果电梯竖直向上做匀加速直线运动,弹簧的伸长量为2 x.求电梯竖直向上加速运动时的加速度.
(2)若斜面不光滑,斜面与物块之间的动摩擦因数为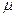 ,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)
,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)