宇航员抵达半径为R的星球表面后,做了如下的实验:取一竖直光滑圆轨道,一质量为m的物体以一定的初速度在竖直平面内做完整的圆周运动,如图所示。测量出当物体运动到圆周的最高点B位置时,物体对轨道的压力为F1;经过最低点A时,物体对轨道的压力为F2。已知引力常量为G,试根据题中所提供的条件和测量结果,求:(不考虑星球的自转)
(1)该星球表面的重力加速度;
(2)该星球的质量M。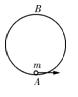
宇航员抵达半径为R的星球表面后,做了如下的实验:取一竖直光滑圆轨道,一质量为m的物体以一定的初速度在竖直平面内做完整的圆周运动,如图所示。测量出当物体运动到圆周的最高点B位置时,物体对轨道的压力为F1;经过最低点A时,物体对轨道的压力为F2。已知引力常量为G,试根据题中所提供的条件和测量结果,求:(不考虑星球的自转)
(1)该星球表面的重力加速度;
(2)该星球的质量M。