如图为某探究活动小组设计的节能运输系统,斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为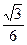 。木箱在轨道顶点时,自动装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速度滑下,当轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端。再重复上述过程。求:(1)
。木箱在轨道顶点时,自动装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速度滑下,当轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端。再重复上述过程。求:(1)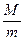 =?
=?
(2)在满足(1)的条件下,若物体下滑的最大距离为L, 则弹簧的最大弹性势能为多大?
则弹簧的最大弹性势能为多大?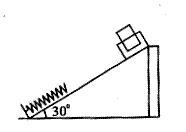
如图为某探究活动小组设计的节能运输系统,斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为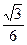 。木箱在轨道顶点时,自动装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速度滑下,当轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端。再重复上述过程。求:(1)
。木箱在轨道顶点时,自动装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速度滑下,当轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端。再重复上述过程。求:(1)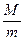 =?
=?
(2)在满足(1)的条件下,若物体下滑的最大距离为L, 则弹簧的最大弹性势能为多大?
则弹簧的最大弹性势能为多大?