如图所示,坐标系xOy位于竖直平面内,在该区域内有场强E=12N/C、方向沿x轴正方向的匀强电场和磁感应强度大小为B=2T、沿水平方向且垂直于xOy平面指向纸里的匀强磁场.一个质量m=4×10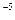 kg,电量q=2.5×10
kg,电量q=2.5×10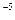 C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10 m/s2,求:
C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10 m/s2,求:
(1)P点到原点O的距离;
(2)带电微粒由原点O运动到P点的时间.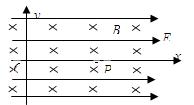
如图所示,坐标系xOy位于竖直平面内,在该区域内有场强E=12N/C、方向沿x轴正方向的匀强电场和磁感应强度大小为B=2T、沿水平方向且垂直于xOy平面指向纸里的匀强磁场.一个质量m=4×10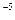 kg,电量q=2.5×10
kg,电量q=2.5×10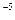 C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10 m/s2,求:
C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.取g=10 m/s2,求:
(1)P点到原点O的距离;
(2)带电微粒由原点O运动到P点的时间.