如图所示,木块A、B与弹簧M拴接,弹簧N的上端与木块B拴接。弹簧M、N的 弹性系数分别为k1、k2,木块A、B的质量分别为m1、m2。木块A的上端用一根细绳通过一定滑轮的缓慢向上提上面的木块A,当弹簧N的下端刚离开地面时,(重力加速度为g)求:
弹性系数分别为k1、k2,木块A、B的质量分别为m1、m2。木块A的上端用一根细绳通过一定滑轮的缓慢向上提上面的木块A,当弹簧N的下端刚离开地面时,(重力加速度为g)求:
(1)木块B移动的距离
(2)木块A移动的距离。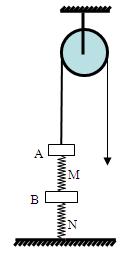
如图所示,木块A、B与弹簧M拴接,弹簧N的上端与木块B拴接。弹簧M、N的 弹性系数分别为k1、k2,木块A、B的质量分别为m1、m2。木块A的上端用一根细绳通过一定滑轮的缓慢向上提上面的木块A,当弹簧N的下端刚离开地面时,(重力加速度为g)求:
弹性系数分别为k1、k2,木块A、B的质量分别为m1、m2。木块A的上端用一根细绳通过一定滑轮的缓慢向上提上面的木块A,当弹簧N的下端刚离开地面时,(重力加速度为g)求:
(1)木块B移动的距离
(2)木块A移动的距离。