如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力).
①在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置坐标.
②在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置坐标应满足的条件.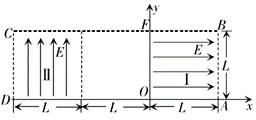
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力).
①在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置坐标.
②在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置坐标应满足的条件.