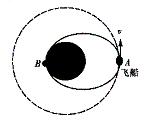
目前,我国正在实施“嫦娥奔月”计划.如图所示,登月飞船以速度v0绕月球做圆周运动,已知飞船质量为m=1.2×104kg,离月球表面的高度为h=100km,飞船在A点突然向前做短时间喷气,喷气的相对速度为u=1.0×104m/s,喷气后飞船在A点的速度减为vA,于是飞船将沿新的椭圆轨道运行,最终飞船能在图中的B点着陆( A.B连线通过月球中心,即A.B两点分别是椭圆的远月点和近月点),试问:
(1)飞船绕月球做圆周运动的速度v0是多大?
(2)由开普勒第二定律可知,飞船在 A.B两处的半径与速率的乘积相等,即rAvA=rBvB,为 使飞船能在B点着陆,喷气时需消耗多少燃料?已知月球的半径为 R=1700km,月球表面的重力加速度为g=1.7m/s2(选无限远处为零势能点,物体的重力势能大小为Ep=
使飞船能在B点着陆,喷气时需消耗多少燃料?已知月球的半径为 R=1700km,月球表面的重力加速度为g=1.7m/s2(选无限远处为零势能点,物体的重力势能大小为Ep=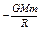 ).
).
 ,下端与大气连通。粗管中有一段水银封闭了一定质量的理想气体,水银柱下表面恰好与粗管和细管的交界处齐平,空气柱和水银柱长度均为h=4cm。现在细管口连接一抽气机(图中未画出),对细管内气体进行缓慢抽气,最终使一半水银进入细管中,水银没有流出细管。已知大气压强为
,下端与大气连通。粗管中有一段水银封闭了一定质量的理想气体,水银柱下表面恰好与粗管和细管的交界处齐平,空气柱和水银柱长度均为h=4cm。现在细管口连接一抽气机(图中未画出),对细管内气体进行缓慢抽气,最终使一半水银进入细管中,水银没有流出细管。已知大气压强为 。
。




 粤公网安备 44130202000953号
粤公网安备 44130202000953号