如图所示,abcd是长为2L、宽为L的长方形区域,该区域内存在垂直于纸面向里匀强磁场,磁感应强度的大小为B。在ab边中点M有一粒子源,该粒子源能不断地向区域内发出质量为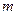 、电量大小为q的带负电的粒子,粒子速度的大小恒定,沿纸面指向各个方向,不计粒子重力。其中垂直于ab边入射的粒子恰能从ad边中点N射出磁场。求:
、电量大小为q的带负电的粒子,粒子速度的大小恒定,沿纸面指向各个方向,不计粒子重力。其中垂直于ab边入射的粒子恰能从ad边中点N射出磁场。求:
(1)粒子入射的速度大小;
(2)bc边有粒子射出的宽度。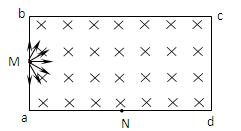
如图所示,abcd是长为2L、宽为L的长方形区域,该区域内存在垂直于纸面向里匀强磁场,磁感应强度的大小为B。在ab边中点M有一粒子源,该粒子源能不断地向区域内发出质量为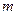 、电量大小为q的带负电的粒子,粒子速度的大小恒定,沿纸面指向各个方向,不计粒子重力。其中垂直于ab边入射的粒子恰能从ad边中点N射出磁场。求:
、电量大小为q的带负电的粒子,粒子速度的大小恒定,沿纸面指向各个方向,不计粒子重力。其中垂直于ab边入射的粒子恰能从ad边中点N射出磁场。求:
(1)粒子入射的速度大小;
(2)bc边有粒子射出的宽度。