如图所示,静止在光滑水平面的木板B的质量 kg、长度L="2.0m." 铁块A静止于木板的右端,其质量
kg、长度L="2.0m." 铁块A静止于木板的右端,其质量 kg,与木板间的动摩擦因数
kg,与木板间的动摩擦因数 ,并可看作质点。现给木板B施加一个水平向右的恒定拉力
,并可看作质点。现给木板B施加一个水平向右的恒定拉力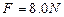 ,使木板从铁块下方抽出,试求:(取g=10m/s2)
,使木板从铁块下方抽出,试求:(取g=10m/s2)
(1)抽出木板所用的时间;
(2)抽出木板时,铁块和木板的速度大小各为多少?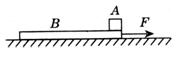
如图所示,静止在光滑水平面的木板B的质量 kg、长度L="2.0m." 铁块A静止于木板的右端,其质量
kg、长度L="2.0m." 铁块A静止于木板的右端,其质量 kg,与木板间的动摩擦因数
kg,与木板间的动摩擦因数 ,并可看作质点。现给木板B施加一个水平向右的恒定拉力
,并可看作质点。现给木板B施加一个水平向右的恒定拉力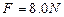 ,使木板从铁块下方抽出,试求:(取g=10m/s2)
,使木板从铁块下方抽出,试求:(取g=10m/s2)
(1)抽出木板所用的时间;
(2)抽出木板时,铁块和木板的速度大小各为多少?