如图甲所示，水平传送带的长度L6m，皮带轮以速度v顺时针匀速

更新 2022-09-03
科目物理
题型计算题
难度中等
浏览 1280

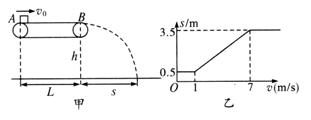
如图甲所示，水平传送带的长度L="6" m，皮带轮以速度v顺时针匀速转动，现在一质量为1 kg的小物体（可视为质点）以水平速度v₀从A点滑上传送带，越过B点后做平抛运动，其水平位移为s，保持物块的初速度v₀不变，多次改变皮带轮的速度v依次测量水平位移s，得到如图乙所示的s-v图象．
（1）当0<v≤l m／s时，物块在A、B之间做什么运动?v≥7 m／s时，物块在A、B之间做什么运动?
（2）物块的初速度v₀多大?

登录免费查看答案和解析

相关试题

有一个1000匝的线圈，在0.4s内通过它的磁通量从0.02Wb均匀增加到0.10Wb,求线圈中的感应电动势。

题型：未知
难度：未知

收藏答案/解析

“10米折返跑”的成绩反映了人体的灵敏素质。测定时，在平直跑道上，受试者以站立式起跑姿势站在起点（终点）线前，听到起跑的口令后，全力跑向正前方10米处的折返线，测试员同时开始计时。受试者到达折返线处，用手触摸折返线处的物体（如木箱）后，再转身跑向起点（终点）线，当胸部到达起点（终点）线的垂直面时，测试员停止计时，所用时间即为“10米折返跑”的成绩，如图所示。设受试者起跑的加速度为4 m/s²，运动过程中的最大速度为4 m/s，快到达折返线处时需减速到零，减速的加速度为8 m/s²，返回时达到最大速度后不需减速，保持最大速度冲线．求该受试者“10米折返跑”的成绩为多少？

题型：未知
难度：未知

收藏答案/解析

一列货车以28.8km/h的速度在铁路上运行，由于调度事故，在后方有一列快车以72km/h的速度在同一轨道上同向驶来，快车司机发现货车时两车相距600m，他立即合上制动器刹车，但快车要滑行2km才能停下，请你判断两车是否会相撞，并说明理由。

题型：未知
难度：未知

收藏答案/解析

一辆汽车在平直公路上匀速行驶，速度大小为v₀=5m/s，关闭油门后汽车的加速度为a=0.5m/s²。求：
（1）4s末汽车的速度；
（2）关闭油门后到汽车位移x=24m所经历的时间t₁；
（3）汽车关闭油门后t₂=12s内滑行的距离。

题型：未知
难度：未知

收藏答案/解析

从离地180m的空中自由落下一个小球，取g=10m/s²，求：
（1）小球经过多少时间落到地面；
（2）小球落地时的速度；
（3）小球落地前最后1s内的位移。

题型：未知
难度：未知

收藏答案/解析

推荐套卷

热门套卷