2007年10月24日,“嫦娥一号”卫星星箭分离,卫星进入绕地球轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④。11月5日11时,当卫星经过距月球表面高度为h的A点时,再一次实施变轨, 进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦。如图所示,已知月球半径为R。
进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦。如图所示,已知月球半径为R。
(1)请回答:“嫦娥一号”在完成第三次近地变轨时需要加速还是减速?
(2)写出月球表面重力加速度的表达式。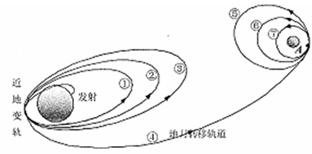
2007年10月24日,“嫦娥一号”卫星星箭分离,卫星进入绕地球轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④。11月5日11时,当卫星经过距月球表面高度为h的A点时,再一次实施变轨, 进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦。如图所示,已知月球半径为R。
进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦。如图所示,已知月球半径为R。
(1)请回答:“嫦娥一号”在完成第三次近地变轨时需要加速还是减速?
(2)写出月球表面重力加速度的表达式。