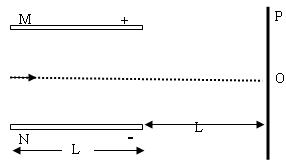
如图所示，M、N为两块水平放置的平行金属板，板长为L，两板间距也为L，板间电压恒定。今有一带负电粒子（重力不计）以一定的初速度沿两板正中间垂直进入电场，最后打在距板右端为L的竖直屏上。粒子落点距O点的距离为L/2。若大量的上述粒子（与原来的初速度一样，并忽略粒子间相互作用力）从两板间不同的位置垂直进入电场。试求这些粒子落在竖直屏上的范围并在图中画出。