如图所示为某公司开发的一款新游戏,竖直平面内ABCD为边长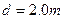 的正方形,AD中点O处有一个子弹弹射装置,可将
的正方形,AD中点O处有一个子弹弹射装置,可将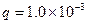 C、
C、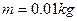 的带正电小球向ABCD区域各方向发射。现在ABCD区域加水平向左的匀强电场,
的带正电小球向ABCD区域各方向发射。现在ABCD区域加水平向左的匀强电场,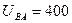 V,图上已标出小球射到正方形不同位
V,图上已标出小球射到正方形不同位 置时对应的得分值。
置时对应的得分值。
(1)某玩家将小球从O点以8m/s射出,正好得60分,则求小球到达C点时的速度大小;
(2)为了获得满分(即射到B点),请你帮玩家设计符合要求的出射速度方向(可用文字描述或用三角函数表示),并给出速度大小需满足的条件。
如图所示为某公司开发的一款新游戏,竖直平面内ABCD为边长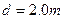 的正方形,AD中点O处有一个子弹弹射装置,可将
的正方形,AD中点O处有一个子弹弹射装置,可将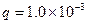 C、
C、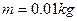 的带正电小球向ABCD区域各方向发射。现在ABCD区域加水平向左的匀强电场,
的带正电小球向ABCD区域各方向发射。现在ABCD区域加水平向左的匀强电场,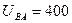 V,图上已标出小球射到正方形不同位
V,图上已标出小球射到正方形不同位 置时对应的得分值。
置时对应的得分值。
(1)某玩家将小球从O点以8m/s射出,正好得60分,则求小球到达C点时的速度大小;
(2)为了获得满分(即射到B点),请你帮玩家设计符合要求的出射速度方向(可用文字描述或用三角函数表示),并给出速度大小需满足的条件。