所示,两木快的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不栓接),整个系统处于平衡状态,现缓慢向上提上面的木块,直到它刚离开上面弹簧,求在这过程中下面木块移动的距离。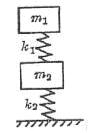
所示,两木快的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不栓接),整个系统处于平衡状态,现缓慢向上提上面的木块,直到它刚离开上面弹簧,求在这过程中下面木块移动的距离。