供电局某工程队在冬天架设电线，如图所示，设两电线杆间距离为L，铜导线总质量为M，电线架好后，在两杆正中部位电线下坠的距离为h，电线在杆上固定处的切线方向与竖直方向的夹角为θ，求：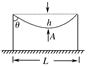
（1）两电线杆处的电线弹力．
（2）当到夏天时，两电线杆处的电线弹力与冬天相比是变大了，还是变小了？为什么？（提示：导线上每处的弹力均沿切线方向）
在范围足够大，方向竖直向下的匀强磁场中，B＝0.2 T，有一水平放置的光滑框架，宽度为L＝0.4 m，如图所示，框架上放置一质量为0.05 kg，电阻为1 Ω的金属杆cd，框架电阻不计．若cd杆以恒定加速度a＝2 m/s2，由静止开始做匀变速运动，则
(1)在5 s内平均感应电动势是多少？
(2)第5 s末，回路中的电流多大？
(3)第5 s末，作用在cd杆上的水平外力多大？
发电站通过升压变压器、输电导线和降压变压器把电能输送到用户(升压变压器和降压变压器都可视为理想变压器)，输电全过程的线路图如图所示，求：
(1)若发电机的输出功率是100 kW，输出电压是250 V，升压变压器的原副线圈的匝数比为1∶25，求升压变压器的输出电压和输电导线中的电流；
(2)若输电导线中的电功率损失为输入功率的4%，求输电导线的总电阻。
如图所示，半径R =" 0.8" m的光滑绝缘导轨固定于竖直平面内，加上某一方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动。圆心O与A点的连线与竖直成一角度θ，在A点时小球对轨道的压力FN="120" N，此时小球动能最大。若小球的最大动能比最小动能多32 J，且小球能够到达轨道上的任意一点（不计空气阻力）。则：
⑴小球的最小动能是多少？
⑵小球受到重力和电场力的合力是多少？
⑶现小球在动能最小的位置突然撤去轨道，并保持其他量都不变，若小球在0.04 s后的动能与它在A点时的动能相等，求小球的质量。
如图所示，跨过轻质定滑轮的细绳两端，一端连接质量为m的物体A，另一端通过一轻质弹簧与质量为M的物体B连接，B物体静止在地面上，用手托着A物体，在A距地面高h处时，细绳刚好被拉直、弹簧无形变。今将A物体从h高处无初速释放，A物体恰好能到达地面，且A到达地面时，B物体对地面的压力恰好减为零。已知重力加速度为g，弹簧的弹性势能与劲度系数k、弹簧的伸长量x的关系是：E弹=
kx2。两个物体均可视为质点，不计绳子和滑轮的质量，不计滑轮轴上的摩擦力和空气阻力。问：
（1）A、B两物体的质量之比为多少?
（2）现将A、B两物体的初始位置互换，再让B物体从h高处无初速释放，当A物体刚要离开地面时，B物体的速度是多少?
粤公网安备 44130202000953号