K—介予方程为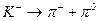 ,其中K-介予和
,其中K-介予和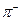 介子是带负电的基元电荷,
介子是带负电的基元电荷,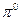 介子不带电。一个K—介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的
介子不带电。一个K—介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的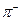 介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径
介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径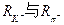 之比为2:1。如图所示,
之比为2:1。如图所示,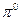 介子的轨迹未画出。由此可知
介子的轨迹未画出。由此可知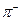 介子的动量大小与
介子的动量大小与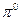 介子的动量大小之比为 ( )
介子的动量大小之比为 ( )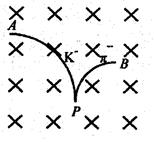
| A.1:1 | B.1:2 | C.1:3 | D.1:6 |
K—介予方程为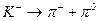 ,其中K-介予和
,其中K-介予和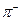 介子是带负电的基元电荷,
介子是带负电的基元电荷,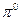 介子不带电。一个K—介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的
介子不带电。一个K—介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的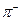 介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径
介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径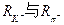 之比为2:1。如图所示,
之比为2:1。如图所示,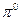 介子的轨迹未画出。由此可知
介子的轨迹未画出。由此可知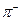 介子的动量大小与
介子的动量大小与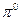 介子的动量大小之比为 ( )
介子的动量大小之比为 ( )
| A.1:1 | B.1:2 | C.1:3 | D.1:6 |