AB是竖直平面内的四分之一圆弧轨道，在下端B与水平直轨道相切，如图所示。一小球自A点起由静止开始沿轨道下滑。已知圆轨道半径为R，小球的质量为m，不计各处摩擦。求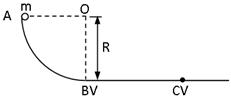
（1）小球运动到B点时的动能
（2）小球下滑到距水平轨道的高度为R时的速度大小和方向
（3）小球经过圆弧轨道的B点和水平轨道的C点时，所受轨道支持力NB、NC各是多大？
相关试题
如图所示，在水平地面上固定一倾角θ=37°、表面光滑且足够长的斜面体，物体A以v1=6m／s的初速度沿斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中。(A、B均可看作质点，sin37°=0.6，cos37°=0.8。g 取10m／s²。)求：
（1）物体A上滑到最高点所用的时间t
（2）物体B抛出时的初速度
（3）物体A、B间初始位置的高度差h
火箭载着宇宙探测器飞向某行星，火箭内平台上还放有测试仪器，如图所示。火箭从地面起飞时，以加速度
竖直向上做匀加速直线运动(
为地面附近的重力加速度)，已知地球半径为R，升到某一高度时，测试仪器对平台的压力刚好是起飞时压力的
，求此时火箭离地面的高度h。
如图质量为m=0.2kg的小球固定在长为L=0.9m的轻杆一端，杆可绕O点的水平转轴在竖直平面内转动，g=10m/s2，求：
（1）小球在最高点的速度v1为多大时，球对杆的作用力为0？
（2）当小球在最高点的速度v2=6m/s时，球对杆的作用力和方向。
有一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥。
（1）汽车到达桥顶时速度为5m/s，汽车对桥的压力是多大？
（2）汽车以多大速度经过桥顶时恰好对桥没有压力而腾空？
粤公网安备 44130202000953号