一个质量m=1kg物体,以初速度v0=4m/s从斜面上A点沿斜面向上运动,物体沿斜面向上运动的最大距离L=1.2m,经过一段时间后物体再返回到A点,此时物体速率vt=2m/s,且返回到A点之前物体已做匀速运动.设斜面的倾角 ,物体与斜面间的动摩擦因数
,物体与斜面间的动摩擦因数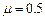 ,物体在运动过程中受到的空气阻力大小与其速率成正比.试求:
,物体在运动过程中受到的空气阻力大小与其速率成正比.试求: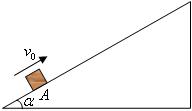
(1)物体在运动过程中受到的空气阻力与速率的比例系数 ;
;
(2)物体刚沿斜面向上运动时的瞬间加速度大小;
(3)物体从开始沿斜面向上运动到返回出发点所用的时间.
一个质量m=1kg物体,以初速度v0=4m/s从斜面上A点沿斜面向上运动,物体沿斜面向上运动的最大距离L=1.2m,经过一段时间后物体再返回到A点,此时物体速率vt=2m/s,且返回到A点之前物体已做匀速运动.设斜面的倾角 ,物体与斜面间的动摩擦因数
,物体与斜面间的动摩擦因数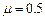 ,物体在运动过程中受到的空气阻力大小与其速率成正比.试求:
,物体在运动过程中受到的空气阻力大小与其速率成正比.试求:
(1)物体在运动过程中受到的空气阻力与速率的比例系数 ;
;
(2)物体刚沿斜面向上运动时的瞬间加速度大小;
(3)物体从开始沿斜面向上运动到返回出发点所用的时间.