如图（甲）是游乐场中双环过山车的实物图片,图（乙）是过山车的原理图。在原理图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道被固定在倾角为α=37°斜直轨道面上的Q、Z两点处（Q、Z是圆轨道的接口，也是轨道间的切点）, 圆形轨道与斜直轨道之间圆滑连接，且在同一竖直面内。PQ之距L1 ="6m," QZ之距L2 =18m，两圆形轨道的最高点A、B均与P点平齐。现使一辆较小的过山车(视作质点)从P点以一定初速度沿斜面向下运动。已知斜轨道面与小车间的动摩擦因数为μ="1/24" , g=10m/s2,sin370 ="0.6" , cos370 =0.8。
（1）若车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
（2）若车在P处的初速度变为10m/s,则小车经过第二个轨道的最低点D处时对轨道的压力是重力的几倍？计算说明车有无可能出现脱轨现象?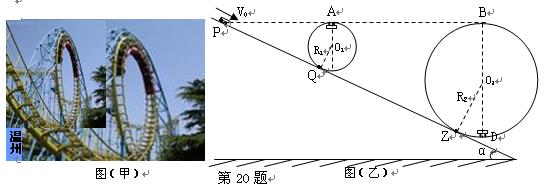
如图是利用传送带装运煤块的示意图．其中传送带长20m，倾角θ=37°，煤块与传送带间的动摩擦因数μ=0.8，传送带的主动轮和从动轮半径相等，主动轮轴顶端与运煤车底板间的竖起高度H=3.2m，与运煤车车箱中心的水平距离x=1.6m．现在传送带底端由静止释放一些煤块（可视为质点），煤块在传送带的作用下先做匀加速直线运动，后与传送带一起做匀速运动，到达主动轮时随轮一起匀速转动．要使煤块在轮的最高点水平抛出并落在车箱中心，取g=10m/s2，sin37°=0.6，cos37°=0.8，求：
（l）传送带匀速运动的速度v及主动轮和从动轮的半径R
（2）煤块在传送带上由静止开始加速至落到车底板所经过的时间T．
现代社会机动车辆越来越多，交通安全日益突出，要求驾驶员一定要遵守交通法规．一辆汽车以10m/s匀速行驶即将通过红绿灯路口，绿灯还有2s熄灭（假设绿灯熄灭红灯立即亮），此时汽车距离停车线26m，并假设前方没有其他车辆．若该汽车加速时最大加速度大小为2m/s2，减速时最大加速度大小为4m/s2．通过计算说明驾驶员应如何操作才能保证安全行驶不违章：是直接加速在红灯之前通过停车线还是减速停车恰好紧靠停车线停下等待下次绿灯？
如图所示，质量为lkg的薄木板静止在光滑水平桌面上，薄木板上有一质量为0.5kg的小铁块，它离木板的左端距离为0.5m，铁块与木板间动摩擦因数为0.1．现用水平拉力向右以2m/s2的加速度将木板从铁块下抽出，求：（不计铁块大小，铁块不滚动，取g=10m/s2）
（1）将木板从铁块下抽出需要多长时间？
（2）水平拉力对木板做的功．
如图是某游乐场的一种过山车的简化图，过山车由倾角为θ的斜面和半径为R的光滑圆环组成0．假设小球从A处由静止释放，沿着动摩擦因数为μ的斜面运动到B点（B为斜面与圆环的切点），而后沿光滑圆环内侧运动，若小球刚好能通过圆环的最高点C，求：（重力加速度为g）
（1）小球沿斜面下滑的加速度的大小；
（2）斜面的长度至少为多大．
粤公网安备 44130202000953号