(16分)如图所示,两根光滑的平行金属导轨处于同一水平面内,相距L=0.3m,导轨的左端M、N用0.2Ω的电阻R连接,导轨电阻不计.导轨上停放着一金属杆,杆的电阻r=0.1 ,质量m=0.1kg,整个装置处于竖直向下的匀强磁场中,磁感应强度B=0.5T 。现在金属杆上施加一垂直于杆的水平向右外力F,使R上的电压每秒钟均匀地增加0.05V,设导轨足够长。
,质量m=0.1kg,整个装置处于竖直向下的匀强磁场中,磁感应强度B=0.5T 。现在金属杆上施加一垂直于杆的水平向右外力F,使R上的电压每秒钟均匀地增加0.05V,设导轨足够长。
(1)证明金属棒做匀加速运动并求出加速度的大小
(2)写出外力F随时间变化的函数式
(3)试求从杆开始运动后的2s内通过电阻R的电量.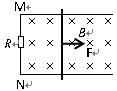
(16分)如图所示,两根光滑的平行金属导轨处于同一水平面内,相距L=0.3m,导轨的左端M、N用0.2Ω的电阻R连接,导轨电阻不计.导轨上停放着一金属杆,杆的电阻r=0.1 ,质量m=0.1kg,整个装置处于竖直向下的匀强磁场中,磁感应强度B=0.5T 。现在金属杆上施加一垂直于杆的水平向右外力F,使R上的电压每秒钟均匀地增加0.05V,设导轨足够长。
,质量m=0.1kg,整个装置处于竖直向下的匀强磁场中,磁感应强度B=0.5T 。现在金属杆上施加一垂直于杆的水平向右外力F,使R上的电压每秒钟均匀地增加0.05V,设导轨足够长。
(1)证明金属棒做匀加速运动并求出加速度的大小
(2)写出外力F随时间变化的函数式
(3)试求从杆开始运动后的2s内通过电阻R的电量.