如图,电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直。当导体棒上升h=3.8m时,获得稳定的速度,导体棒上产生的热量为2J,电动 机牵引棒时,电压表、电流表
机牵引棒时,电压表、电流表 的读数一直为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:
的读数一直为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:
(1)棒能达到的稳定速度;
(2)棒从静止至达到稳定速度所需要 的时间。
的时间。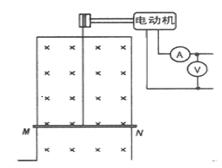
如图,电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升,导体棒的电阻R为1Ω,架在竖直放置的框架上,它们处于磁感应强度B为1T的匀强磁场中,磁场方向与框架平面垂直。当导体棒上升h=3.8m时,获得稳定的速度,导体棒上产生的热量为2J,电动 机牵引棒时,电压表、电流表
机牵引棒时,电压表、电流表 的读数一直为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:
的读数一直为7V、1A,电动机内阻r为1Ω,不计框架电阻及一切摩擦,求:
(1)棒能达到的稳定速度;
(2)棒从静止至达到稳定速度所需要 的时间。
的时间。