如图所示,矩形ABCD为长方体水池横截面,宽度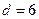 m,高
m,高 m,水池里装有高度为
m,水池里装有高度为 m、折射率为
m、折射率为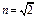 的某种液体,在水池底部水平放置宽度
的某种液体,在水池底部水平放置宽度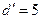 m的平面镜,水池左壁高
m的平面镜,水池左壁高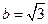 m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度。
m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度。
如图所示,矩形ABCD为长方体水池横截面,宽度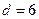 m,高
m,高 m,水池里装有高度为
m,水池里装有高度为 m、折射率为
m、折射率为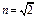 的某种液体,在水池底部水平放置宽度
的某种液体,在水池底部水平放置宽度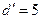 m的平面镜,水池左壁高
m的平面镜,水池左壁高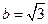 m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度。
m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度。