如图所示,一质量为m的滑块以大小为v0的速度经过水平直轨道上的a点滑行距离为s后开始沿竖直平面的半圆形轨道运动,滑块与水平直轨道间的动摩擦因数为μ,水平直轨道与半圆形轨道相切连接,半圆形轨道半径为R,滑块到达半圆形轨道最高点b时恰好不受压力.试求:
(1)滑块刚进入和刚离开半圆形轨道时的速度;
(2)滑块落回到水平直轨道时离a点的距离.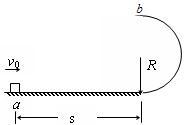
如图所示,一质量为m的滑块以大小为v0的速度经过水平直轨道上的a点滑行距离为s后开始沿竖直平面的半圆形轨道运动,滑块与水平直轨道间的动摩擦因数为μ,水平直轨道与半圆形轨道相切连接,半圆形轨道半径为R,滑块到达半圆形轨道最高点b时恰好不受压力.试求:
(1)滑块刚进入和刚离开半圆形轨道时的速度;
(2)滑块落回到水平直轨道时离a点的距离.