如图所示,质量m1="0.3" kg 的小车静止在光滑的水平面上,车长L="15" m,现有质量m2="0.2" kg可视为质点的物块,以水平向右的速度v0="2" m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数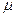 =0.5,取g="10" m/s2.求
=0.5,取g="10" m/s2.求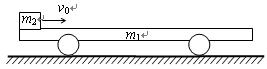
(1)物 块在车面上滑行的时间t;
块在车面上滑行的时间t; (2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0′不超过多少.
(2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0′不超过多少.
如图所示,质量m1="0.3" kg 的小车静止在光滑的水平面上,车长L="15" m,现有质量m2="0.2" kg可视为质点的物块,以水平向右的速度v0="2" m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数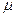 =0.5,取g="10" m/s2.求
=0.5,取g="10" m/s2.求
(1)物 块在车面上滑行的时间t;
块在车面上滑行的时间t; (2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0′不超过多少.
(2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0′不超过多少.