|
如图12所示，厚度为h，宽度为d的导体板放在垂直于它的磁感应强度为B的匀强磁场中，当电流通过导体板时，在导体板的上侧面A和下侧面A’会产生电势差。这种现象称为霍尔效应。实验表明，当磁场不太强时，电势差U、电流I的B的关系为：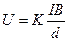
式中的比例系数K称为霍尔系数。霍尔效应可解释如下：外部磁场的洛仑兹力使运动的电子聚集在导体板的一侧，在导体板的另一侧会出现多余的正电荷，从而形成横向电场。横向电场对电子施加与洛仑兹力方向相反的静电力。当静电力与洛仑兹力达到平衡时，导体板上下两侧之间就会形成稳定的电势差。
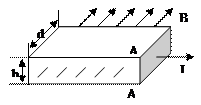
（1）稳定状态时，导体板上侧面A的电势 下侧面A’的电势（填高于、低于或等于）
（2）电子所受洛仑兹力的大小为
（3）当导体板上下两侧之间的电势差为U时，电子所受的静电力为 。
一列简谐横波沿x轴正方向传播，位于原点的质点的振动图象如图12－2－8甲所示．
(1)该振动的振幅是________cm；
(2)振动的周期是________s；
(3)在t等于
周期时，位于原点的质点离开平衡位置的位移是________cm.
图乙所示为该波在某一时刻的波形图，A点位于x＝0.5 m处．
(4)该波的传播速度是________m/s；
(5)经过
周期后，A点离开平衡位置的位移是________cm.
弹性绳沿x轴放置，左端位于坐标原点，用手握住绳的左端，当t＝0时使其开始沿y轴做振幅为8 cm的简谐振动，在t＝0.25 s时，绳上形成如图12－2－7所示的波形，则该波的波速为________cm/s；在t＝________s时，位于x2＝45 cm处的质点N恰好第一次沿y轴正向通过平衡位置．
如图12－2－6所示为某一简谐横波在t＝0时刻的波形图，由此可知该波沿________方向传播，该时刻a、b、c三点中速度最大的是________点，加速度最大的是________点，从这一时刻开始，第一次最快回到平衡位置的是________点，若t＝0.02 s时，质点c第一次到达波谷处，则此波的波速为________m/s.
如图12－2－5所示为声波干涉演示仪的原理图．两个U形管A和B套在一起，A管两侧各有一小孔．声波从左侧小孔传入管内，被分成两列频率________的波．当声波分别通过A、B传播到右侧小孔时，若两列波传播的路程相差半个波长，则此处声波的振幅________；若传播的路程相差一个波长，则此处声波的振幅________．
粤公网安备 44130202000953号