如图,在竖直平面内有两平行金属导轨AB、CD。导轨间距为L,电阻不计。一根电阻不计的金属棒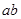 可在导轨上无摩擦地滑动。棒
可在导轨上无摩擦地滑动。棒 与导轨垂直,并接触良好。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B。导轨右边与电路连接。电路中的两个定值电阻分别为2R和R。在BD间接有一水平放置的平行板电容器C,板间距离为d。当
与导轨垂直,并接触良好。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B。导轨右边与电路连接。电路中的两个定值电阻分别为2R和R。在BD间接有一水平放置的平行板电容器C,板间距离为d。当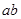 以速度
以速度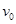 匀速向左运动时,电容器中质量为m的带电微粒恰好静止。求:微粒的带电性质,及带电量的大小。
匀速向左运动时,电容器中质量为m的带电微粒恰好静止。求:微粒的带电性质,及带电量的大小。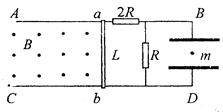
如图,在竖直平面内有两平行金属导轨AB、CD。导轨间距为L,电阻不计。一根电阻不计的金属棒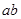 可在导轨上无摩擦地滑动。棒
可在导轨上无摩擦地滑动。棒 与导轨垂直,并接触良好。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B。导轨右边与电路连接。电路中的两个定值电阻分别为2R和R。在BD间接有一水平放置的平行板电容器C,板间距离为d。当
与导轨垂直,并接触良好。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B。导轨右边与电路连接。电路中的两个定值电阻分别为2R和R。在BD间接有一水平放置的平行板电容器C,板间距离为d。当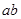 以速度
以速度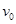 匀速向左运动时,电容器中质量为m的带电微粒恰好静止。求:微粒的带电性质,及带电量的大小。
匀速向左运动时,电容器中质量为m的带电微粒恰好静止。求:微粒的带电性质,及带电量的大小。