在某平面上有一半径为R的圆形区域,区域内外均有垂直于该平面的匀强磁场,圆外磁场范围足够大,已知两部分磁场方向相反且磁感应强度都为B,方向如图所示。现在圆形区域的边界上的A点有一个电量为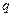 ,质量为
,质量为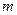 的带电粒子以沿半径且垂直于磁场方向向圆外的速度经过该圆形边界,已知该粒子只受到磁场对它的作用力。
的带电粒子以沿半径且垂直于磁场方向向圆外的速度经过该圆形边界,已知该粒子只受到磁场对它的作用力。
若粒子在其与圆心O连线旋转一周时恰好能回到A点,试救济 粒子运动速度V的可能值。
在粒子恰能回到A点的情况下,求该粒子回到A点所需的最短时间。
在某平面上有一半径为R的圆形区域,区域内外均有垂直于该平面的匀强磁场,圆外磁场范围足够大,已知两部分磁场方向相反且磁感应强度都为B,方向如图所示。现在圆形区域的边界上的A点有一个电量为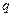 ,质量为
,质量为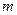 的带电粒子以沿半径且垂直于磁场方向向圆外的速度经过该圆形边界,已知该粒子只受到磁场对它的作用力。
的带电粒子以沿半径且垂直于磁场方向向圆外的速度经过该圆形边界,已知该粒子只受到磁场对它的作用力。
若粒子在其与圆心O连线旋转一周时恰好能回到A点,试救济 粒子运动速度V的可能值。
在粒子恰能回到A点的情况下,求该粒子回到A点所需的最短时间。