竖直平面内有一形状为抛物线的光滑曲面轨道,如图12-3-15所示,抛物线方程是y=x2,轨道下半部分处在一个水平向外的匀强磁场中,磁场的上边界是y=a的直线(图中虚线所示),一个小金属环从抛物线上y=b(b＞a)处以速度v沿抛物线下滑,假设抛物线足够长,金属环沿抛物线下滑后产生的焦耳热总量是( )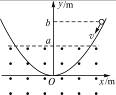
图12-3-15
| A．mgb | B． |
C．mg(b－a) | D． |
竖直平面内有一形状为抛物线的光滑曲面轨道,如图12-3-15所示,抛物线方程是y=x2,轨道下半部分处在一个水平向外的匀强磁场中,磁场的上边界是y=a的直线(图中虚线所示),一个小金属环从抛物线上y=b(b＞a)处以速度v沿抛物线下滑,假设抛物线足够长,金属环沿抛物线下滑后产生的焦耳热总量是( )
图12-3-15
| A．mgb | B． |
C．mg(b－a) | D． |
粤公网安备 44130202000953号