如图15-3-12所示的磁电式电流表的内部示意图.已知辐射状磁场的磁感应强度B="0.9" T,矩形线圈边长L1="2" cm,L2="2.5" cm,匝数N="2" 000,电流表的满偏角为θ=90°,与线圈相连的两个螺旋弹簧总的扭转特征是:每扭转1°,产生的力矩为1×10-6 N·m.求该电流表的满偏电流.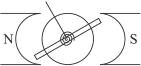
图15-3-12
相关试题
电磁炮是一种理想的兵器，它的主要原理如图11-2-13所示，1982年澳大利亚国立大学制成了能把2.2g的炮体(包括金属杆MN的质量)加速到10km／s的电磁炮，若轨道宽为2m，长为100m，通过的电流为10A，则轨道间所加匀强磁场的磁感应强度B为多少?(不计摩擦)
已知如图，水平放置的平行金属板间有匀强电场。一根长l的绝缘细绳一端固定在O点，另一端系有质量为m并带有一定电荷的小球。小球原来静止在C点。当给小球一个水平冲量后，它可以在竖直面内绕O点做匀速圆周运动。若将两板间的电压增大为原来的3倍，求：要使小球从C点开始在竖直面内绕O点做圆周运动，至少要给小球多大的水平冲量？在这种情况下，在小球运动过程中细绳所受的最大拉力是多大？
某一电动机，当电压U1=10V时带不动负载，因此不转动，这时电流为I1=2A。当电压为U2=36V时能带动负载正常运转，这时电流为I2=1A。求这时电动机的机械功率是多大？
如图所示，有一提升重物用的直流电动机，内阻r="0.6" Ω， R="10" Ω，U="160" V，电压表的读数为110 V，求
（1）通过电动机的电流是多少？
（2）输入到电动机的电功率是多少？
（3）在电动机中发热的功率是多少？
（4）电动机工作1 h所产生的热量是多少？
粤公网安备 44130202000953号