有一只电压表,量程已知,内阻为RV,另有一蓄电池(电动势未知,但不超过电压表的量程,内阻可忽略),请用这只电压表和蓄电池,再用一个单刀双掷开关和一些连接导线,设计测量某一高值电阻Rx的实验方法(已知Rx的值与RV相差不大)。
(1) 在甲图的方框内,画出实验电路图;
在甲图的方框内,画出实验电路图;
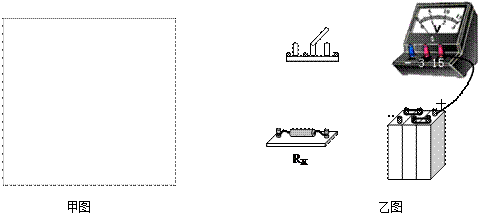
(2)请用笔画线代替导线连接如图乙所示的实物图(其中部分已连好);
(3)简要写出实验的主要步骤,并根据实验测得的数据,推导出高值电阻Rx的表达式。
有一只电压表,量程已知,内阻为RV,另有一蓄电池(电动势未知,但不超过电压表的量程,内阻可忽略),请用这只电压表和蓄电池,再用一个单刀双掷开关和一些连接导线,设计测量某一高值电阻Rx的实验方法(已知Rx的值与RV相差不大)。
(1) 在甲图的方框内,画出实验电路图;
在甲图的方框内,画出实验电路图;
(2)请用笔画线代替导线连接如图乙所示的实物图(其中部分已连好);
(3)简要写出实验的主要步骤,并根据实验测得的数据,推导出高值电阻Rx的表达式。