如图 1-6-7 所示，静止在光滑水平面上的小车质量为 M="20" kg.从水枪中喷出的水柱的横截面积为 S="10" m2，速度为 v="10" m/s，水的密度为ρ=1.0×103 kg/m3.若用水枪喷出的水从车后沿水平方向冲击小车的前壁，且冲击到小车前壁的水全部沿前壁流进小车中.当有质量为 m="5" kg 的水进入小车时，试求：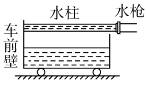
图1-6-7
（1）小车的速度大小；
（2）小车的加速度大小.
如图 1-6-7 所示，静止在光滑水平面上的小车质量为 M="20" kg.从水枪中喷出的水柱的横截面积为 S="10" m2，速度为 v="10" m/s，水的密度为ρ=1.0×103 kg/m3.若用水枪喷出的水从车后沿水平方向冲击小车的前壁，且冲击到小车前壁的水全部沿前壁流进小车中.当有质量为 m="5" kg 的水进入小车时，试求：
图1-6-7
（1）小车的速度大小；
（2）小车的加速度大小.
粤公网安备 44130202000953号