如图18-3-8所示,半径为r且水平放置的光滑绝缘的环形管道内,有一个电荷量为e,质量为m的电子.此装置放在匀强磁场中,其磁感应强度随时间变化的关系式为B=B0+kt(k>0).根据麦克斯韦电磁场理论,均匀变化的磁场将产生稳定的电场,该感应电场对电子将有沿圆环切线方向的作用力,使其得到加速.设t=0时刻电子的初速度大小为v0,方向顺时针,从此开始运动一周后的磁感应强度为B1,则此时电子的速度大小为( )
图18-3-8
A.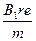 |
B.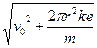 |
C.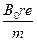 |
D. |
相关知识点
如图18-3-8所示,半径为r且水平放置的光滑绝缘的环形管道内,有一个电荷量为e,质量为m的电子.此装置放在匀强磁场中,其磁感应强度随时间变化的关系式为B=B0+kt(k>0).根据麦克斯韦电磁场理论,均匀变化的磁场将产生稳定的电场,该感应电场对电子将有沿圆环切线方向的作用力,使其得到加速.设t=0时刻电子的初速度大小为v0,方向顺时针,从此开始运动一周后的磁感应强度为B1,则此时电子的速度大小为( )
图18-3-8
A.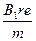 |
B.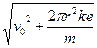 |
C.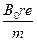 |
D. |