如图12-3-5所示,沿波的传播方向上有间距均为1 m的六个质点a、b、c、d、e、f。均静止在各自平衡位置,一列横波以1 m/s的速度水平向右传播,t=0时到达质点a,质点a开始由平衡位置向上运动,t="1" s时,质点a第一次到达最高点,则在4 s<t<5 s这段时间内( )
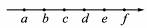
图12-3-5
| A.质点c的加速度逐渐增大 | B.质点a的速度逐渐增大 |
| C.质点c向下运动 | D.质点f保持静止 |
如图12-3-5所示,沿波的传播方向上有间距均为1 m的六个质点a、b、c、d、e、f。均静止在各自平衡位置,一列横波以1 m/s的速度水平向右传播,t=0时到达质点a,质点a开始由平衡位置向上运动,t="1" s时,质点a第一次到达最高点,则在4 s<t<5 s这段时间内( )
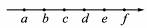
图12-3-5
| A.质点c的加速度逐渐增大 | B.质点a的速度逐渐增大 |
| C.质点c向下运动 | D.质点f保持静止 |