如图5-4-4所示，有一连通器，左右两管的横截面积均为S，内盛密度为ρ的液体.开始时两管内的液面高度差为h，若打开底部中央的阀门K，液体开始流动，最终两液面相平.在这一过程中，液体的重力势能变化了多少？是增加了还是减少了？如果是减少了，减少的重力势能到哪里去了？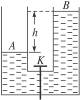
图5-4-4
相关试题
如图所示，两条固定的光滑的平行长金属导轨PQ和MN相距L＝2m，电阻忽略不计。两导轨在同一水平面上，导轨上放有两根电阻均为r＝1Ω且与导轨垂直的细金属杆ab和cd，处在竖直向上的磁感应强度B＝0.5T的匀强磁场中，杆cd系一细绳，绳跨过定滑轮与地面上一质量m＝1kg的重物相连，不计绳与滑轮以及滑轮与轴间的摩擦。最初ab、cd均静止，且细绳绷直但无张力。t=0时刻，ab从静止开始以2m/s2加速度向左做匀加速直线运动，
求：（1）t=2s末绳的张力大小？
（2）若t时刻物体离开地面，求t值。（g＝10m/s2）
的导体棒置于磁感应强度
的匀强磁场中，使导体棒和磁场方向垂直，如图所示若导体棒中的电流
，方向向左，则导体棒受到的安培力大小为多少？安培力的方向如何？
如图6—8（a）所示，跨过定滑轮的轻绳两端的物体A和B的质量分别为M和m，物体A 在水平面上。A由静止释放，当B沿竖直方向下落h时，测得A沿水平面运动的速度为v，这时细绳与水平面的夹角为θ，试分析计算B下降h过程中，地面摩擦力对A做的功？（滑轮的质量和摩擦均不计）
如图6—4所示，河宽为L，船对水的速度为V船，水的流速为V水，试分析：
（1）船怎样渡河，所需时间最短？最短时间为多少？
（2）当V船>V水时，船怎样渡河位移最小？最小位移是多少？
（3）当V水<V船时，船怎样渡河位移最小？最小位移是多少？
=0.2，小车足够长.求
粤公网安备 44130202000953号