面积很大的水池,水深为H,水面上浮着一正方体木块,木块边长为a,密度为水的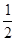 ,质量为m.开始时,木块静止,有一半没入水中,如图7-5-11所示,现用力F将木块缓慢地压到池底,不计摩擦.求:从木块刚好完全没入水中到停止在池底的过程中,池水势能的改变量.
,质量为m.开始时,木块静止,有一半没入水中,如图7-5-11所示,现用力F将木块缓慢地压到池底,不计摩擦.求:从木块刚好完全没入水中到停止在池底的过程中,池水势能的改变量.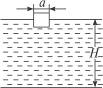
图7-5-11
面积很大的水池,水深为H,水面上浮着一正方体木块,木块边长为a,密度为水的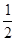 ,质量为m.开始时,木块静止,有一半没入水中,如图7-5-11所示,现用力F将木块缓慢地压到池底,不计摩擦.求:从木块刚好完全没入水中到停止在池底的过程中,池水势能的改变量.
,质量为m.开始时,木块静止,有一半没入水中,如图7-5-11所示,现用力F将木块缓慢地压到池底,不计摩擦.求:从木块刚好完全没入水中到停止在池底的过程中,池水势能的改变量.
图7-5-11