如图7-7-13连接而成，列车从斜轨高处无动力静止滑下，经过圆轨道后再冲上另一斜轨.已知列车质量为m，圆轨道半径为R.若将列车看成质点，并且不计摩擦，求：
(1)要保证列车能安全通过圆轨道，则斜轨高度至少多大；
(2)若列车较长，不能看成质点，并且要考虑列车与轨道间的摩擦，则对斜轨高度有何影响.
(3)若列车由许多节构成，总长恰为2πR，列车高度不计，摩擦阻力也不考虑，为保证列车能安全通过圆轨道，求斜轨高度至少多大.
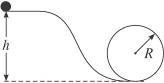
图7-7-13
如图(a)所示，两块水平放置的平行金属板A、B，板长L＝18.5cm，两板间距d＝3cm，两板之间有垂直于纸面向里的匀强磁场，磁感应强度B＝6.0×10－2T，两板加上如图(b)所示的周期性电压，带电时A板带正电．当t＝0时，有一个质量m＝1.0×10－12kg，带电荷量q＝＋1.0×10－6C的粒子，以速度v＝600m/s，从距A板2.5cm处，沿垂直于磁场、平行于两板的方向射入两板之间，若不计粒子的重力，取π＝3.0，求：
(1)粒子在0～1×10－4s内做怎样的运动？位移多大？
(2)带电粒子从射入到射出板间所用的时间．
如图(甲)所示，两水平放置的平行金属板C、D相距很近，上面分别开有小孔O和
，水平放置的平行金属导轨P、Q与金属板C、D接触良好，且导轨在磁感应强度为B1＝10T的匀强磁场中，导轨间距L＝0.50m．金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动．其速度图像如图(乙)，若规定向右运动速度方向为正方向，从t＝0时刻开始，由C板小孔O处连续不断飘入质量为m＝3.2×10－21kg、电量q＝1.6×10－19C的带正电的粒子(设飘入速度很小，可视为零)．在D板外侧有以MN为边界的匀强磁场B2＝10T，MN与D相距d＝10cm，B1和B2方向如图(甲)所示(粒子重力及其相互作用不计)，求：
(1)0～4.0s时间内哪些时刻发射的粒子能穿过电场并飞出磁场边界MN？
(2)粒子从边界MN射出来的位置之间最大的距离为多少？
如图1(a)所示，在空间存在一个变化的电场和一个变化的磁场，电场的方向水平向右(图中由B到C)，场强的大小变化如图1(b)所示，磁感应强度变化如图1(c)所示，方向垂直于纸面，从t＝1s末开始，在A点每隔2s有一个相同的带电粒子(重力不计)沿AB方向(垂直于BC)的速度v0射出，恰好能击中C点，若AC＝2BC，且粒子在AC间的运动时间小于1s，求：
(1)图像中E0和B0的比值；
(2)磁场的方向；
(3)若第一个粒子击中C点的时刻已知为(1＋Δt)s，则第二个粒子击中C点的时刻是多少？
如下图所示，在直角坐标系的第一、二象限内有垂直于纸面的勾强磁场，第三象限有沿Y轴负方向的匀强电场，第四象限内无电场和磁场．质量为m、带电量为q的粒子从M点以速度v0沿X轴负方向进入电场，不计粒子的重力，粒子经N、和X轴上的P点最后又回到M点．设OM＝OP＝l，ON＝2l，求：
(1)电场强度E的大小．
(2)匀强磁场的磁感强度B的大小和方向．
(3)粒子从M点进入电场，经N、P点最后又回到M点所用的时间．
穿过中间磁场，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面．求：
粤公网安备 44130202000953号