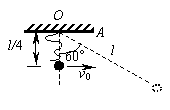
如图所示，长为l的轻绳一端系于固定点O，另一端拴一个质量为m的小球。将小球从O点正下方l/4处以一定的初速度v0水平向右抛出。经过一段时间，绳被拉直，在极短的时间内小球的速度变为0，此后小球以O为悬点在竖直平面内摆动。已知绳刚被拉直时与竖直方向成60°角。求
①小球水平抛出时的初速度v0。
②在绳被拉直的短暂过程中，悬点O受到绳拉力的冲量。
如图12所示，质量为mb=14kg的木板B放在水平地面上，
质量为ma=10kg的木箱A放在木板B上.一根轻绳一端拴在木箱
上，另一端拴在地面的木桩上，绳绷紧时绳与水平面的夹角为
=37°，已知木箱A与木板B之间的动摩擦因数
=0.5，木板B
与地面之间动摩擦因数
=0.4.重力加速度g =10m/s2. 现用水平力F将木板B从木箱A下面匀速抽出.(sin370＝0.6 cos370＝0.8)，求：
(1) 绳上张力T的大小；
(2) 拉力F的大小。
磁悬浮列车是一种高速低耗的新型交通工具，它的驱动系统简化为如下模型，固定在列车下端的动力绕组可视为一个矩形纯电阻金属框，电阻为，金属框置于
平面内，长边
为
平行于
轴，宽为
的
边平行于
轴，如图l所示。列车轨道沿
方向，轨道区域内存在垂直于金属框平面的磁场，磁感应强度
沿
方向按正弦规律分布，其空间周期为
，最大值为
，如图2所示，金属框同一长边上各处的磁感应强度相同，整个磁场以速度
沿
方向匀速平移。设在短暂时间内，
、
边所在位置的磁感应强度随时问的变化可以忽略，并忽略一切阻力。列车在驱动系统作用下沿
方向加速行驶，某时刻速度为
（）
（1）简要叙述列车运行中获得驱动力的原理；
（2）为使列车获得最大驱动力，写出、
边应处于磁场中的什么位置及
与
之间应满足的关系式；
（3）计算在满足第（2）问的条件下列车速度为v时驱动力的大小。
光滑水平面上放着质量，1kg的物块A与质量
2kg的物块
，
与
均可视为质点，
靠在竖直墙壁上，
、
间夹一个被压缩的轻弹簧（弹簧与
、
均不拴接），用手挡住
不动，此时弹簧弹性势能
49J。在
、
间系一轻质细绳，细绳长度大于弹簧的自然长度，如图所示。放手后
向右运动，绳在短暂时间内被拉断，之后
冲上与水平面相切的竖直半圆光滑轨道，其半径
0.5m, B恰能到达最高点
。取
10m/s2，求：
（1）绳拉断后瞬间的速度
的大小；
（2）绳拉断过程绳对的冲量
的大小；
（3）绳拉断过程绳对所做的功
。
在平面直角坐标系中，第Ⅰ象限存在沿
轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为
。一质量为
、电荷量为
的带正电的粒子从
轴正半轴上的
点以速度
垂直于
轴射入电场，经
轴上的
点与
轴正方向成
角射入磁场，最后从
轴负半轴上的
点垂直于
轴射出磁场，如图所示。不计粒子重力，求：
（1）、
两点间的电势差
；
（2）粒子在磁场中运动的轨道半径；
（3）粒子从点运动到P点的总时间
。
粤公网安备 44130202000953号