一辆摩托车能达到的最大速度为vm=30m/s,要想在3分钟内由静止起沿一条平直公路追上在前面1000m处正以v0=20m/s的速度匀速行驶的汽车,则摩托车必须以多大的加速度起动?
一位同学的解法是:设摩托车正好在3分内追上汽车,摩托车和汽车的位移分别是:
S摩=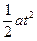 ,S汽=
,S汽=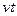 ,而S摩=S汽+S0,t=180秒,S0=1000米,
,而S摩=S汽+S0,t=180秒,S0=1000米,
……
你认为该同学的解法正确吗?若正确请完成此题;若错误请说明理由,并按正确的解法完成此题。
相关知识点
一辆摩托车能达到的最大速度为vm=30m/s,要想在3分钟内由静止起沿一条平直公路追上在前面1000m处正以v0=20m/s的速度匀速行驶的汽车,则摩托车必须以多大的加速度起动?
一位同学的解法是:设摩托车正好在3分内追上汽车,摩托车和汽车的位移分别是:
S摩=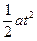 ,S汽=
,S汽=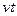 ,而S摩=S汽+S0,t=180秒,S0=1000米,
,而S摩=S汽+S0,t=180秒,S0=1000米,
……
你认为该同学的解法正确吗?若正确请完成此题;若错误请说明理由,并按正确的解法完成此题。