如图所示,带电粒子以平行于极板的速度从左侧中央射入匀强电场,恰好能从右侧擦极板边缘射出电场(不计粒子的重力).如果粒子的动能变为原来的两倍,要使它们仍能擦极板边缘飞出,则可以采取的措施有( )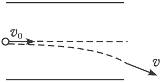
| A.将极板的长度变为原来的2倍 | B.将极板的间距变为原来的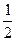 |
| C.将两极板之间的电压变为原来的2倍 | D.以上措施均不对 |
如图所示,带电粒子以平行于极板的速度从左侧中央射入匀强电场,恰好能从右侧擦极板边缘射出电场(不计粒子的重力).如果粒子的动能变为原来的两倍,要使它们仍能擦极板边缘飞出,则可以采取的措施有( )
| A.将极板的长度变为原来的2倍 | B.将极板的间距变为原来的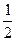 |
| C.将两极板之间的电压变为原来的2倍 | D.以上措施均不对 |