一卫星绕某行星做匀速圆周运动,已知行星表面的重力加速度为g行,行星的质量M与卫星的质量m之比M/m=81,行星的半径R行与卫星的半径R卫之比R行/R卫=3.6,行星与卫星之间的距离r与行星的半径R行之比r/R行=60.设卫星表面的重力加速度为g卫,则在卫星表面有: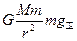
……
经过计算得出:卫星表面重力加速度为行星表面重力加速度的1/3 600.上述结果是否正确?若正确,列式证明;若错误,求出正确结果.
一卫星绕某行星做匀速圆周运动,已知行星表面的重力加速度为g行,行星的质量M与卫星的质量m之比M/m=81,行星的半径R行与卫星的半径R卫之比R行/R卫=3.6,行星与卫星之间的距离r与行星的半径R行之比r/R行=60.设卫星表面的重力加速度为g卫,则在卫星表面有: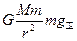
……
经过计算得出:卫星表面重力加速度为行星表面重力加速度的1/3 600.上述结果是否正确?若正确,列式证明;若错误,求出正确结果.