如图所示,边长为a的等边三角形区域内有匀强磁场B,方向垂直纸面向外,边长也是a的等边三角形导体框架ABC,在t=0时恰好与磁场的边界重合,而后以周期T绕其中心顺时针方向匀速旋转,于是框架ABC中有感应电流.规定电流按A-B-C-A方向流动时电流为正值,反向流动时为负值.设框架ABC的总电阻为R,试求t=0到t1=T/6时间内平均电流 和从t=0到t1=T/2时间内平均电流
和从t=0到t1=T/2时间内平均电流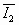 .
.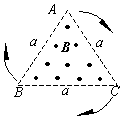
如图所示,边长为a的等边三角形区域内有匀强磁场B,方向垂直纸面向外,边长也是a的等边三角形导体框架ABC,在t=0时恰好与磁场的边界重合,而后以周期T绕其中心顺时针方向匀速旋转,于是框架ABC中有感应电流.规定电流按A-B-C-A方向流动时电流为正值,反向流动时为负值.设框架ABC的总电阻为R,试求t=0到t1=T/6时间内平均电流 和从t=0到t1=T/2时间内平均电流
和从t=0到t1=T/2时间内平均电流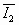 .
.