如图所示，质量为m=10kg的两个相同的物块A、B(它们之间用轻绳相连)放在水平地面上，在方向与水平方面成
角斜向上、大小为100N的拉力F作用下，以大小为
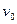=4． 0m／s的速度向右做匀速直线运动，求剪断轻绳后物块A在水平地面上滑行的距离。(取当地 的重力加速度g=10m/s2，sin37
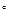=0．6，cos37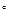=0．8)
相关试题
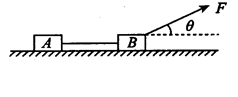
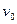如图所示，质量为m=10kg的两个相同的物块A、B(它们之间用轻绳相连)放在水平地面上，在方向与水平方面成角斜向上、大小为100N的拉力F作用下，以大小为=4． 0m／s的速度向右做匀速直线运动，求剪断轻绳后物块A在水平地面上滑行的距离。(取当地 的重力加速度g=10m/s2，sin37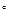=0．6，cos37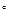=0．8)
的均质小球放在倾角为
的光滑斜面上，并被斜面上一个竖直的光滑挡板挡住，处于静止状态，试求小球对挡板和斜面的压力（已知
）
电场强度E的大小和方向；
粤公网安备 44130202000953号