“S”形玩具轨道如图所示.该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内.轨道弯曲部分是由两个半径相等的半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切.弹射装置将一个直径略小于细管直径的小球(可视为质点)从a点水平射向b点并进入轨道,经过轨道后从P点水平抛出.已知小球与地面ab段间的动摩擦因数 ,ab段长L=2.25m,半圆的半径R=0.1m,不计其它机械能损失,g取10m/s2,若
,ab段长L=2.25m,半圆的半径R=0.1m,不计其它机械能损失,g取10m/s2,若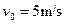 ,求:
,求:
(1)小球到达b点时的速度vb;
(2)小物体从P点抛出后的水平射程.
“S”形玩具轨道如图所示.该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内.轨道弯曲部分是由两个半径相等的半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切.弹射装置将一个直径略小于细管直径的小球(可视为质点)从a点水平射向b点并进入轨道,经过轨道后从P点水平抛出.已知小球与地面ab段间的动摩擦因数 ,ab段长L=2.25m,半圆的半径R=0.1m,不计其它机械能损失,g取10m/s2,若
,ab段长L=2.25m,半圆的半径R=0.1m,不计其它机械能损失,g取10m/s2,若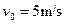 ,求:
,求:
(1)小球到达b点时的速度vb;
(2)小物体从P点抛出后的水平射程.