如图所示,水平放置的两平行金属板M、N间的距离d=0.20m,给两板加电压U(M板带正电荷,N板带负电荷),板间有一长度L=0.10m的绝缘狭板AB能够绕点A在竖直平面内转动。先使AB板保持水平静止,并在AB的中点放一个质量m=4.9× kg,电荷量q=9×
kg,电荷量q=9× C的带正电荷的微粒P(重力忽略不计)。使板AB突然以角速度ω=100πrad/s沿顺时针方向匀速转动,为使板AB在转动中能与微粒P相碰,求加在平行金属板M、N之间的电压的取值范围。
C的带正电荷的微粒P(重力忽略不计)。使板AB突然以角速度ω=100πrad/s沿顺时针方向匀速转动,为使板AB在转动中能与微粒P相碰,求加在平行金属板M、N之间的电压的取值范围。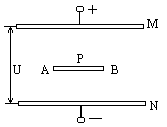
相关知识点
如图所示,水平放置的两平行金属板M、N间的距离d=0.20m,给两板加电压U(M板带正电荷,N板带负电荷),板间有一长度L=0.10m的绝缘狭板AB能够绕点A在竖直平面内转动。先使AB板保持水平静止,并在AB的中点放一个质量m=4.9× kg,电荷量q=9×
kg,电荷量q=9× C的带正电荷的微粒P(重力忽略不计)。使板AB突然以角速度ω=100πrad/s沿顺时针方向匀速转动,为使板AB在转动中能与微粒P相碰,求加在平行金属板M、N之间的电压的取值范围。
C的带正电荷的微粒P(重力忽略不计)。使板AB突然以角速度ω=100πrad/s沿顺时针方向匀速转动,为使板AB在转动中能与微粒P相碰,求加在平行金属板M、N之间的电压的取值范围。