已知地球质量为M、半径为R，万有引力常量G．卫星在地球表面绕地球做匀速圆周运动所需的速度称为第一宇宙速度v1,卫星从地面发射，恰好能脱离地球引力束缚的速度称为第二宇宙速度v2，已知v2=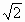
v1．根据以上条件，并以卫星脱离地球引力时的引力势能为0，求质量为m的卫星在地球表面时的引力势能．(忽略空气阻力的影响)
相关试题
已知地球质量为M、半径为R，万有引力常量G．卫星在地球表面绕地球做匀速圆周运动所需的速度称为第一宇宙速度v1,卫星从地面发射，恰好能脱离地球引力束缚的速度称为第二宇宙速度v2，已知v2=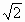v1．根据以上条件，并以卫星脱离地球引力时的引力势能为0，求质量为m的卫星在地球表面时的引力势能．(忽略空气阻力的影响)
，2s后匀减速到36
的均质小球放在倾角为
的光滑斜面上，并被斜面上一个竖直的光滑挡板挡住，处于静止状态，试求小球对挡板和斜面的压力（已知
）
粤公网安备 44130202000953号