如图11(甲)所示为学校操场上一质量不计的竖直滑竿,滑竿上端固定,下端悬空。为了研究学生沿竿的下滑情况,在竿顶部装有一拉力传感器,可显示竿顶端所受拉力的大小。现有一学生(可视为质点)从上端由静止开始滑下,5s末滑到竿底时速度恰好为零。以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图11(乙)所示,g取10m/s2。求:
(1)该学生下滑过程中的最大速率?
(2)滑竿的长度为多少?
(3)1s末到5s末传感器显示的拉力为多少?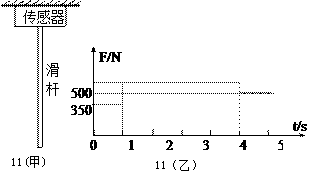
如图11(甲)所示为学校操场上一质量不计的竖直滑竿,滑竿上端固定,下端悬空。为了研究学生沿竿的下滑情况,在竿顶部装有一拉力传感器,可显示竿顶端所受拉力的大小。现有一学生(可视为质点)从上端由静止开始滑下,5s末滑到竿底时速度恰好为零。以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图11(乙)所示,g取10m/s2。求:
(1)该学生下滑过程中的最大速率?
(2)滑竿的长度为多少?
(3)1s末到5s末传感器显示的拉力为多少?