如图所示,倾角a = 37°的固定斜面上放一块质量M =" 1" kg,长度 L =" 3" m的薄平板AB。平板的上表面光滑,其下端B与斜面底端C的距离为7m。在平板的上端A处放一质量m = 0.6kg的滑块,开始时使平板和滑块都静止,之后将它们无初速释放。假设平板与斜面间、滑块与斜面间的动摩擦因数均为m = 0.5,求滑块、平板下端B到达斜面底端C的时间差是多少?(sin37 ="0.6 " cos37
="0.6 " cos37 ="0.8 " g=10m/s
="0.8 " g=10m/s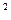 )
)

如图所示,倾角a = 37°的固定斜面上放一块质量M =" 1" kg,长度 L =" 3" m的薄平板AB。平板的上表面光滑,其下端B与斜面底端C的距离为7m。在平板的上端A处放一质量m = 0.6kg的滑块,开始时使平板和滑块都静止,之后将它们无初速释放。假设平板与斜面间、滑块与斜面间的动摩擦因数均为m = 0.5,求滑块、平板下端B到达斜面底端C的时间差是多少?(sin37 ="0.6 " cos37
="0.6 " cos37 ="0.8 " g=10m/s
="0.8 " g=10m/s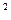 )
)
