如图12所示,在竖直平面内有一圆形绝缘轨道,半径R=1m,处于垂直于轨道平面向里的匀强磁场中,一质量为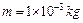 ,带电量为
,带电量为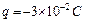 的小球,可在内壁滑动。现在最低点处给小球一个水平初速度v0,使小球在竖直平面内逆时针做圆周运动,图13甲是小球在竖直平面内的速率v随时间变化的情况,图13乙是小球所受轨道的弹力F随时间变化的情况,已知小球能
的小球,可在内壁滑动。现在最低点处给小球一个水平初速度v0,使小球在竖直平面内逆时针做圆周运动,图13甲是小球在竖直平面内的速率v随时间变化的情况,图13乙是小球所受轨道的弹力F随时间变化的情况,已知小球能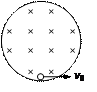
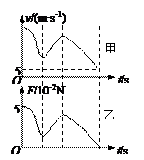
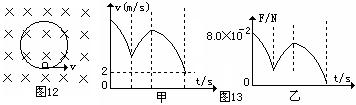
有两次到达圆形轨道的最高点。结合图象和数据(g="10" m/s2),求:
(1)磁感应强度的大小;
(2)小球从开始运动至图甲中速度为2m/s的过程中,摩擦力对小球做的功。
如图12所示,在竖直平面内有一圆形绝缘轨道,半径R=1m,处于垂直于轨道平面向里的匀强磁场中,一质量为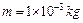 ,带电量为
,带电量为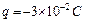 的小球,可在内壁滑动。现在最低点处给小球一个水平初速度v0,使小球在竖直平面内逆时针做圆周运动,图13甲是小球在竖直平面内的速率v随时间变化的情况,图13乙是小球所受轨道的弹力F随时间变化的情况,已知小球能
的小球,可在内壁滑动。现在最低点处给小球一个水平初速度v0,使小球在竖直平面内逆时针做圆周运动,图13甲是小球在竖直平面内的速率v随时间变化的情况,图13乙是小球所受轨道的弹力F随时间变化的情况,已知小球能
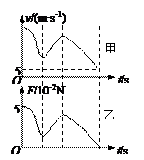

有两次到达圆形轨道的最高点。结合图象和数据(g="10" m/s2),求:
(1)磁感应强度的大小;
(2)小球从开始运动至图甲中速度为2m/s的过程中,摩擦力对小球做的功。