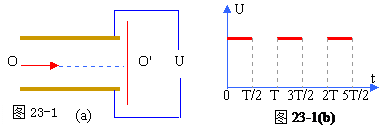
两平行金属板相距为d，加上如图23-1(b)所示的方波形电压，电压的最大值为U0，周期为T。现有一离子束，其中每个离子的质量为m，电量为q，从与两板等距处沿着与板平行的方向连续地射入两板间的电场中。设离子通过平行板所需的时间恰为 T(与电压变化周期相同)，且所有离子都能通过两板间的空间打在右端的荧光屏上。试求：离子击中荧光屏上的位置的范围。(也就是与O‘点的最大距离与最小距离)。重力忽略不计。